Angle Sum Property of a Triangle is the special property of a triangle that is used to find the value of an unknown angle in the triangle. It is the most widely used property of a triangle and according to this property, “Sum of All the Angles of a Triangle is equal to 180º.”
Angle Sum Property of a Triangle is applicable to any of the triangles whether it is a right, acute, obtuse angle triangle or any other type of triangle. So, let’s learn about this fundamental property of a triangle i.e., “Angle Sum Property “.
Table of Content
- What is the Angle Sum Property?
- Angle Sum Property Formula
- Proof of Angle Sum Property
- Exterior Angle Property of a Triangle Theorem
- Angle Sum Property of Triangle Facts
- Solved Example
- FAQs
What is the Angle Sum Property?
For a closed polygon, the sum of all the interior angles is dependent on the sides of the polygon. In a triangle sum of all the interior angles is equal to 180 degrees. The image added below shows the triangle sum property in various triangles.
.webp)
This property holds true for all types of triangles such as acute, right, and obtuse-angled triangles, or any other triangle such as equilateral, isosceles, and scalene triangles. This property is very useful in finding the unknown angle of the triangle if two angles of the triangle are given.
Angle Sum Property Formula
The angle sum property formula used for any polygon is given by the expression,
Sum of Interior Angle = (n − 2) × 180°
where ‘n’ is the number of sides of the polygon.
According to this property, the sum of the interior angles of the polygon depends on how many triangles are formed inside the polygon, i.e. for 1 triangle the sum of interior angles is 1×180° for two triangles inside the polygon the sum of interior angles is 2×180° similarly for a polygon of ‘n’ sides, (n – 2) triangles are formed inside it.
Example: Find the sum of the interior angles for the pentagon.
Solution:
Pentagon has 5 sides.
So, n = 5
Thus, n – 2 = 5 – 2 = 3 triangles are formed.
Sum of Interior Angle = (n − 2) × 180°
⇒ Sum of Interior Angle = (5 − 2) × 180°
⇒ Sum of Interior Angle = 3 × 180° = 540°
Proof of Angle Sum Property
Theorem 1: The angle sum property of a triangle states that the sum of interior angles of a triangle is 180°.
Proof:
The sum of all the angles of a triangle is equal to 180°. This theorem can be proved by the below-shown figure.
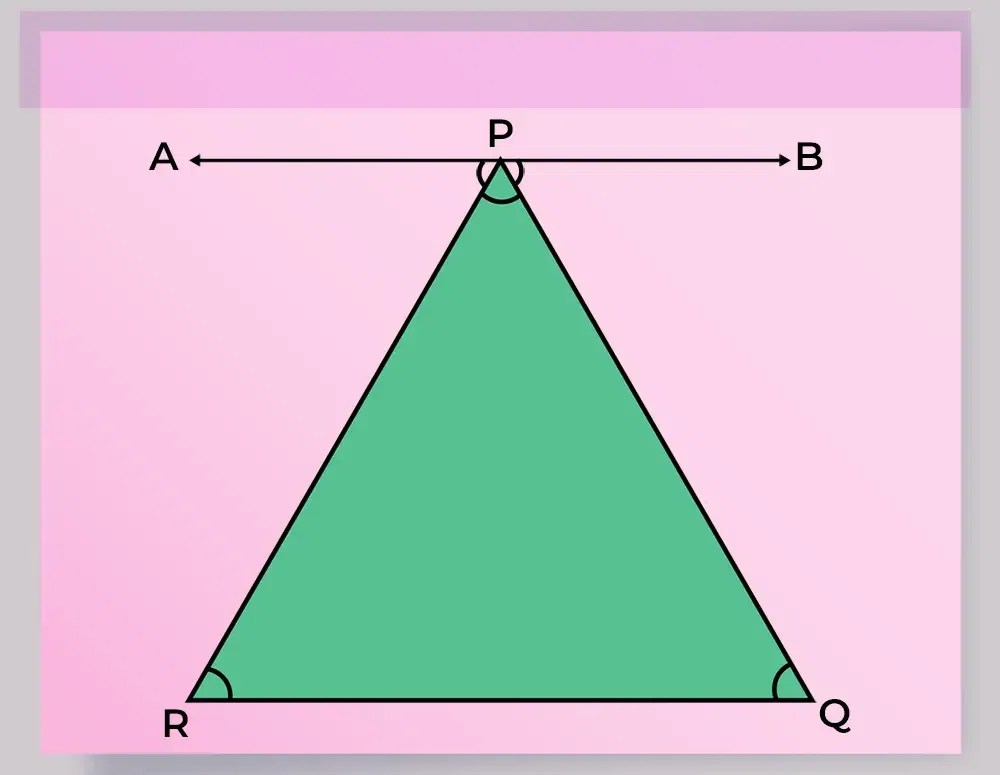
Follow the steps given below to prove the angle sum property in the triangle.
Step 1: Draw a line parallel to any given side of a triangle let’s make a line AB parallel to side RQ of the triangle.
Step 2: We know that sum of all the angles in a straight line is 180°. So, ∠APR + ∠RPQ + ∠BPQ = 180°
Step 3: In the given figure as we can see that side AB is parallel to RQ and RP, and QP act as a transversal. So we can see that angle ∠APR = ∠PRQ and ∠BPQ = ∠PQR by the property of alternate interior angles we have studied above.
From step 2 and step 3,
∠PRQ + ∠RPQ + ∠PQR = 180° [Hence Prooved]
Example: In the given triangle PQR if the given is ∠PQR = 30°, ∠QRP = 70°then find the unknown ∠RPQ
Solution:
As we know that, sum of all the angle of triangle is 180°
∠PQR + ∠QRP + ∠RPQ = 180°
⇒ 30° + 70° + ∠RPQ = 180°
⇒ 100° + ∠RPQ = 180°
⇒ ∠RPQ = 180° – 100°
⇒ ∠RPQ = 80°
Exterior Angle Property of a Triangle Theorem
Theorem 2: If any side of a triangle is extended, then the exterior angle so formed is the sum of the two opposite interior angles of the triangle.
Proof:
As we have proved the sum of all the interior angles of a triangle is 180° (∠ACB + ∠ABC + ∠BAC = 180°) and we can also see in figure, that ∠ACB + ∠ACD = 180° due to the straight line. By the above two equations, we can conclude that
∠ACD = 180° – ∠ACB
⇒ ∠ACD = 180° – (180° – ∠ABC – ∠CAB)
⇒ ∠ACD = ∠ABC + ∠CAB
Hence proved that If any side of a triangle is extended, then the exterior angle so formed is the sum of the two opposite interior angles of the triangle.
Example: In the triangle ABC, ∠BAC = 60° and ∠ABC = 70° then find the measure of angle ∠ACB.
Solution:
The solution to this problem can be approached in two ways:
Method 1: By angle sum property of a triangle we know ∠ACB + ∠ABC + ∠BAC = 180°
So therefore ∠ACB = 180° – ∠ABC – ∠BAC
⇒ ∠ACB = 180° – 70° – 60°
⇒ ∠ACB = 50°
And ∠ACB and ∠ACD are linear pair of angles,
⇒ ∠ACB + ∠ACD = 180°
⇒ ∠ACD = 180° – ∠ACB = 180° – 50° = 130°
Method 2: By exterior angle sum property of a triangle, we know that ∠ACD = ∠BAC + ∠ABC
∠ACD = 70° + 60°
⇒ ∠ACD = 130°
⇒ ∠ACB = 180° – ∠ACD
⇒ ∠ACB = 180° – 130°
⇒ ∠ACB = 50°
Read More about Exterior Angle Theorem.
Angle Sum Property of Triangle Facts
Various interesting facts related to the angle sum property of the triangles are,
- Angle sum property theorem holds true for all the triangles.
- Sum of the all the exterior angles of the triangle is 360 degrees.
- In a triangle sum of any two sides is always greater than equal to the third side.
- A rectangle and square can be divided into two congruent triangles by their diagonal.
Also, Check
- Area of a Triangle
- Area of Isosceles Triangle
Solved Example on Angle Sum Property of a Triangle
Example 1: It is given that a transversal line cuts a pair of parallel lines and the ∠1: ∠2 = 4: 5 as shown in figure 9. Find the measure of the ∠3?
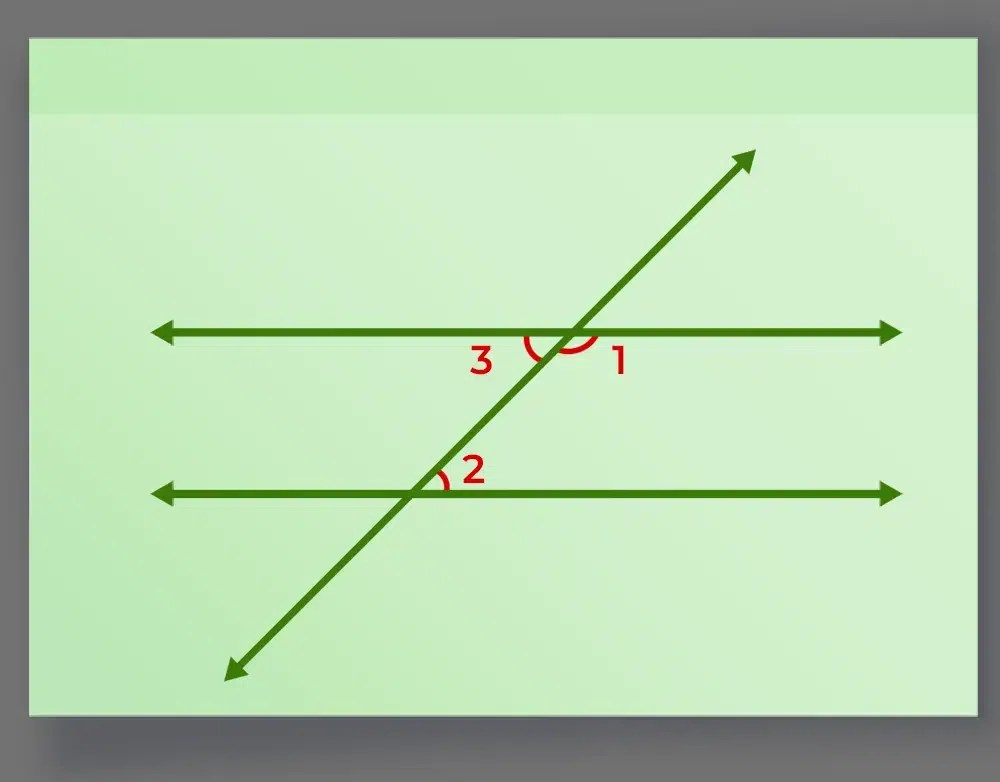
Solution:
As we are given that the given pair of a line are parallel so we can see that ∠1 and ∠2 are consecutive interior angles and we have already studied that consecutive interior angles are supplementary.
Therefore let us assume the measure of ∠1 as ‘4x’ therefore ∠2 would be ‘5x’
Given, ∠1 : ∠2 = 4 : 5.
∠1 + ∠2 = 180°
⇒ 4x + 5x = 180°
⇒ 9x = 180°
⇒ x = 20°
Therefore ∠1 = 4x = 4 × 20° = 80° and ∠2 = 5x = 5 × 20° = 100°.
As we can clearly see in the figure that ∠3 and ∠2 are alternate interior angles so ∠3 = ∠2
∠3 = 100°.
Example 2: As shown in Figure below angle APQ=120° and angle QRB=110°. Find the measure of the angle PQR given that the line AP is parallel to line RB.
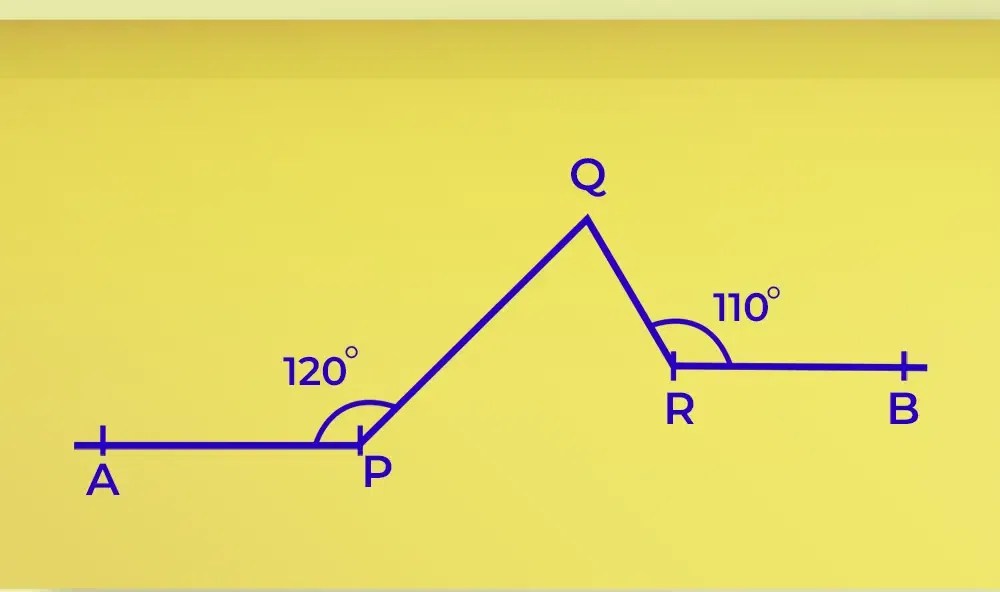
Solution:
As we are given that line AP is parallel to line RB
We know that the line perpendicular to one would surely be perpendicular to the other. So let us make a line perpendicular to both the parallel line as shown in the picture.
Now as we can clearly see that
∠APM + ∠MPQ = 120° and as PM is perpendicular to line AP so ∠APM = 90° therefore,
⇒ ∠MPQ = 120° – 90° = 30°.
Similarly, we can see that ∠ORB = 90° as OR is perpendicular to line RB therefore,
∠QRO = 110° – 90° = 20°.
Line OR is parallel to line QN and MP therefore,
∠PQN = ∠MPQ as they both are alternate interior angles. Similarly,
⇒ ∠NQR = ∠ORQ
Thus, ∠PQR = ∠PQN + ∠NQR
⇒ ∠PQR = 30° + 20°
⇒ ∠PQR = 50°
FAQs on Angle Sum Property
Define Angle Sum Property of a Triangle.
Angle Sum Property of a triangle states that the sum of all the interior angles of a triangle is equal to 180°. For example, In a triangle PQR, ∠P + ∠Q + ∠R = 180°.
What is the Angle Sum Property of a Polygon?
The angle sum property of a Polygon states that for any polygon with side ‘n’ the sum of all its interior angle is given by,
Sum of all the interior angles of a polygon (side n) = (n-2) × 180°
What is the use of the angle sum property?
The angle sum property of a triangle is used to find the unknown angle of a triangle when two angles are given.
Who discovered the angle sum property of a triangle?
The proof for triangle sum property was first published by, Bernhard Friedrich Thibaut in the second edition of his Grundriss der Reinen Mathematik
What is the Angle Sum Property of a Hexagon?
Angle sum property of a hexagon, states that the sum of all the interior angles of a hexagon is 720°.
sahivam4u
Improve
Previous Article
Transversal Lines
Next Article
Triangles in Geometry
.webp)